AQUASPLATCHE

A program to simulate genetic diversity based on a realistic vectorized environment

Introduction

Classical models of structured populations do not apply well to populations of freshwater fishes, since they evolve in complex networks of river systems that are intermediate between one-dimensional and two-dimensional stepping-stone models. In order to allow the simulation of the genetic diversity of populations drawn from such river systems, we have developed a new simulation program called AQUASPLATCHE. It starts by dividing a realistic vectorized network of river streams into segments of arbitrary length. The program then proceeds by simulating the colonization of the streams from an arbitrary source, recording the evolution of the segment densities and the migration events between adjacent segments over time. This demographic history is then used to generate genetic data of population samples located in various segments of the river system, using a backward coalescent framework.

Demographic and spatial expansion module

Principles
The demographic and spatial expansion module allows to simulate a demographic and spatial expansion from one or more initial populations. The simulation uses discrete time and space. The unit of time is the generation, while the unit of the space is a segment, also called a deme. Each segment has a certain length and can be considered as a homogeneous subpopulation. Each segment undergoes an independent population growth and can exchange emigrants with its direct neighboring demes. Each segment is also considered as a sub-unit of the environment. Variations through time of the range extension are also possible, which is defined as a dynamic environment.

Demographic model
The demographic models consist of two steps:

Regulation phase
At each generation and for each segment there is first a logistic regulation of the population size following the equation

.

K is the carrying capacity for a segment, N is the population size of the segment and r is the growth rate.

Migration phase
The regulation phase is directly followed by a migration phase where individuals are exchanged between neighboring segments. To take into account that species may show a different migration behavior during the colonization phase compared to in the equilibrium phase when habitats are already colonized, we introduced a density based migration rate m_D changing smoothly between low and high local densities.

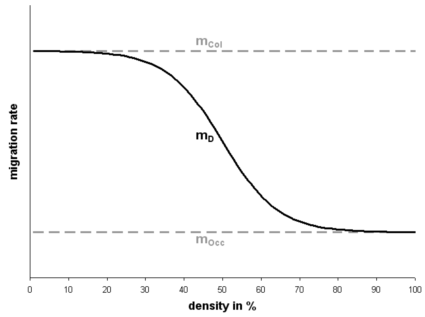
Figure 1. Migration rate m_D depending on the local density. m_Col is the given migration rate at low density and m_Occ is the given migration rate at high densities. In this figure m_Col is bigger than m_Occ implying that this species migrates faster during the colonization process compared to the equilibrium phase.

The corresponding equation is

,

where m_Col is the migration rate during the colonization phase (un-colonization habitats), m_Occ is the migration rate during the equilibrium phase (colonized habitats), D is the current local density defined as N/K (population size divided by the carrying capacity), A is an absolute term set to 1000, and L is L=2*ln(A). The bigger A is, the smoother the migration curve is. L is calculated in order that the mean value between the two migration rates corresponds to a density of 50%. If m_Col is bigger than m_Occ the migration rate is higher during colonization and vise versa if m_Col is smaller than m_Occ. If the two migration rates are equal the migration rate is constant for all densities. The number of emigrants M is then distributed among the neighboring segments taking into account the neighboring segment densities D_i. The probability of sending emigrants is calculated as

,

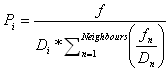whereas neighboring segments at low population densities are favored to obtain immigrants compared to neighboring segments at high population densities. The parameter f represents the directional migration and depends on the physical position the neighboring segment (neig) has in relation to the local segment (loc):

,

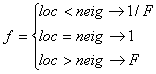where “loc < neig” means that the local segment is physically below the neighboring segment (downstream) and consequently the water flows from the neighboring to the current segment. F is the probability of upstream migration compared to downstream migration (upstream migration/downstream migration), which has to be specified. If F>1 then upstream migration is more probable than downstream migration and the opposite is true for F<1. If F=1 then the species has no preferences for directional migration.

The effective numbers of emigrants send to neighboring segment i is

.

Genetic Module

Principles
The genetic simulation procedure is implemented according to the program SPLATCHE (Currat et al., 2004), with some modifications when generating microsatellite data. Genetic simulations are always preceded by a demographic simulation as they use the demographic information stored in the data base generated during the demographic phase. The genetic phase is based on the “coalescent theory”, initially described by Kingman (1982a; 1982b) and developed in following papers (Ewens, 1990; Hudson, 1990; Donnelly & Tavaré, 1995). This theory allows the reconstruction of the genealogy of a series of sampled genes until their most recent common ancestor (MRCA). For neutral genes, the genealogy essentially depends on the demographic factors that have influenced the history of the populations from whom the genes are drawn. The implementation of the coalescent theory is a modified version of SIMCOAL (Excoffier et al., 2000). The principal difference with SIMCOAL is that the demographic information used by genetic simulations does not come from the “migration matrix” and "historical events" anymore, but from the data base generated during the demographic simulation.

The genetic simulation itself follows the procedure described in Excoffier et al. (2000) and consists in two phases:

 1°) Reconstruction of the genealogy:
The reconstruction of the genealogy is independent on the mutational process. Basically, a number n of genes is chosen. These genes are only identified by their number and they have no genetic variability during this first phase. All the n genes are associated with a geographic position in the virtual river system where the demography is simulated. These genes could belong to different segments in the river system. Then, going backward in time, the genealogy of these genes is reconstructed until their most recent common ancestor (MRCA) in the following way:

Going backward in time, at each generation, two events can occur:

• Coalescent event: If at least two genes are in the same segment, they can potentially have a common ancestor at the preceding generation (a so-called coalescent event). This probability depends on the population size of the segment where the genes are located. Each pair of genes has a probability 1/N_i of coalescence (if N_i is the number of haploid individual in the segment i). If there are n_i genes on the segment then the probability of one coalescent event becomes n_i (n_i -1)/2N_i. Only one coalescent event is allowed per segment and per generation (see Ray et al. (2003) for a discussion about this assumption).

• Migration: Each gene could have arrived with an immigrant from a different segment. When going backward in time, it means that the gene could leave the current segment with the immigrant. So, the probability of migration from a segment i to a segment j for a gene depends on the number of individuals that have arrived from segment j to segment i at this generation. For each gene belonging to the segment i, the probability of migration from segment j is equal to m_ji/N_i where m_ji is the number of immigrants from segment j to segment i during the demographic phase. All the segment densities and the numbers of immigrant between segments are taken from the database generated during the demographic simulation.

2°) Generation of the genetic diversity:
The second phase of a genetic simulation consists in generating the genetic diversity of the samples. This operation is done by adding independent mutations over the branches of the genealogy assuming a uniform and constant Poisson process. At the end of this process all sampled genes have a specific genetic identity. The genetic process is entirely stochastic.
The coalescent backward approach does not generate the history of the whole population, but only that of sampled genes and their ancestors. Thus this approach is much less demanding in terms of memory and computation time. It allows the simulation of complex demographic scenarios within a very broad geographical and temporal framework.

Genetic data
Different types of molecular data can be generated (Microsatellites, RFLP, DNA, Standard, and SNP), each with its own specificities:

Microsatellite data
A generalized stepwise mutation model (GSM, Zhivotovsky et al., 1997; Estoup et al., 2002) is implemented, with or without constraint on the total size of the microsatellite. Several fully linked microsatellite loci can be simulated under the same mutation model constraints. The output for each loci is listed as a number of repeat, having started arbitrarily at 5,000 repeats. The number of repeats for each gene should thus be centered around that value of 5,000.

RFLP data
Only a pure 2-allele model is implemented. Several fully linked RFLP loci can be simulated, assuming a homogeneous mutational process over all loci. A finite-sites model is used, and mutations can hit the same site several times, switching the RFLP site on and off. We thus assume that there is the same probability for a site loss or for a site gain.

DNA sequence data
Several simple finite-sites mutational models are implemented. The user can specify the percentage of substitutions that are transitions (the transition bias), the amount of heterogeneity in mutation rates along a DNA sequence according to either a discrete or continuous Gamma distribution. We can therefore simulate DNA sequences under a Jukes and Cantor model (Jukes & Cantor, 1969) or under a Kimura-2-parameter model (Kimura, 1980), with or without Gamma correction for heterogeneity of mutation rates (Jin & Nei, 1990). Other mutation models that depend on the nucleotide composition of the sequence were not considered here, because of their complexity and because they require specifying many additional parameters, like the mutation transition matrix and the equilibrium nucleotide composition.

Standard data
Following the definition given in ARLEQUIN User Manual (Schneider et al., 2000) this type defines data for which the molecular basis is not particularly defined, such as mere allele frequencies. The comparison between alleles is done at each locus. For each locus, the alleles could be either similar or different.

SNP data
SNP data consist in loci with two different states: ancestral (0) and mutant (1). There is no information about the molecular difference between the 2 states. It is possible in AQUASPLATCHE to specify a minimum frequency for the minor allele (the less frequent of the 2 states) over all samples or at least within one sample.

References
-Currat, M., N. Ray, et al. (2004). Splatche: a program to simulate genetic diversity taking into account environmental heterogeneity, Molecular Ecology Notes, Volume 4, Issue 1, Page 139-142
-Donnelly, P. and S. Tavaré (1995). "Coalescents and genealogical structure under neutrality." Annu. Rev. Genet. 29: 401-421.
-Estoup A., P. Jarne , J. M. Cornuet (2002). "Homoplasy and mutation model at microsatellite loci and their consequences for population genetics analysis". Molecular Ecology 11, 1591-1604.
-Ewens, W. J. (1990). Population Genetics Theory - The Past and the Future. Mathematical and Statistical developments of Evolutionary Theory. S. Lessar. Dordrecht, Kluwer Academic Publishers: 177-227.
-Excoffier, L., J. Novembre, et al. (2000). "SIMCOAL: A general coalescent program for the simulation of molecular data in interconnected populations with arbitrary demography." J. Heredity 91: 506-510.
-Hudson, R. (1990). Gene genealogies and the coalescent process. oxford, Oxford University Press.
-Jin, L. and M. Nei (1990). "Limitations of the evolutionary parsimony method of phylogenetic analysis." Mol. Biol. Evol. 7: 82-102.
-Jukes, T. and C. Cantor (1969). Evolution of protein molecules. Mamalian Protein Metabolism. H. N. Munro. New York, Academic press: 21-132.
-Kimura, M. (1980). "A simple method for estimating evolutionary rate of base substitution through comparative studies of nucleotide sequences." J. Mol. Evol. 16: 111-120.
-Kingman, J. F. C. (1982). "The coalescent." Stoch. Proc. Appl. 13: 235-248.
-Kingman, J. F. C. (1982). "On the genealogy of large populations." J. Appl. Proba. 19A: 27-43.
-Ray, N., M. Currat, et al. (2003). "Intra-deme molecular diversity in spatially expanding populations." Molecular Biology and Evolution 20(1): 76-86.
-Schneider, S., D. Roessli, et al. (2000). Arlequin: a software for population genetics data analysis. User manual ver 2.000. Geneva, Genetics and Biometry Lab, Dept. of Anthropology, University of Geneva.
-Zhivotovsky, L. A., M. W. Feldman , S. A. Grishechkin (1997). "Biased mutations and microsatellite variation." Molecular Biology and Evolution 14, 926-933

Installation

There are several versions of AQUASPLATCHE available. The described installation procedure is for the graphical version for Windows.

1. Download AQUASPLATCHE to any temporary directory.

2. Extract all files contained in the compressed file to a directory of your choice.

3. Start AQUASPLATCHE by double-clicking on the file AquaSplatche.exe, which is the main executable file.

4. Reading the manual helps to get familiar with AQUASPLATCHE

Downloads

	Download AQUASPLATCHE for Windows (graphical version)
	Download AQUASPLATCHE for Windows (consol version)
	Download AQUASPLATCHE for Linux (consol version)
	Download user manual (pdf)

This software was developed by Samuel Neuenschwander and the reference to cite is:
Neuenschwander S (2006) AQUASPLATCHE: a program to simulate genetic diversity in populations living in linear habitats. Molecular Ecology Notes 6 583-585.

Screenshots

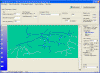
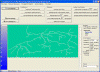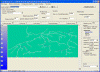
File & Image settings	Network transformation	Demographic simulation settings
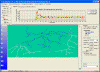
Genetic simulation settings	Time Series

Acknowledgment

I am grateful to Laurent Excoffier, Mathias Currat, and Nicolas Ray for sharing ideas and pieces of code with me. This work was supported by a Swiss NSF grant no. 3100A0-100800 to Laurent Excoffier.

Contact: Samuel Neuenschwander, Computational and Molecular Population Genetics Lab, University of Bern, Switzerland

Last edited on 16.08.06 (13:08)